Ортогональность двух векторов – это одно из фундаментальных понятий в линейной алгебре и геометрии. Она отражает непосредственную связь между векторами, определяющую их взаимное расположение в пространстве. Проверка ортогональности векторов является важным шагом в решении многих задач, в том числе геометрических и физических.
Существуют несколько методов для проверки ортогональности двух векторов. Один из самых простых и наиболее распространенных методов – это вычисление скалярного произведения векторов. Если скалярное произведение равно нулю, то векторы ортогональны друг другу. Этот метод основывается на определении ортогональности через угол между векторами.
Другой метод для проверки ортогональности – это использование матриц. Покажем на примере. Пусть у нас есть два вектора A = (a1, a2, a3) и B = (b1, b2, b3). Превратим их в матрицу размером 3 на 1: A = [[a1],[a2],[a3]] и B = [[b1],[b2],[b3]]. Затем перемножим матрицы A и B с транспонированной матрицей B. Если полученная матрица равна нулевой матрице, то векторы ортогональны.
Методы проверки ортогональности векторов

Существует несколько методов для проверки ортогональности векторов:
- Вычисление скалярного произведения: Скалярное произведение двух векторов можно вычислить по формуле: а · b = |a| * |b| * cos(θ), где а и b - векторы, |a| и |b| - их длины, а θ - угол между ними. Если скалярное произведение равно нулю, то векторы ортогональны.
- Проверка с помощью ортогональных свойств: Некоторые векторы могут обладать определенными ортогональными свойствами. Например, векторы, перпендикулярные плоскости, ортогональны друг другу. Или векторы, направленные вдоль координатных осей, также являются ортогональными.
- Графический метод: Векторы можно изобразить на плоскости или в пространстве и визуально оценить их ортогональность. Если векторы пересекаются под прямым углом или они параллельны осям координат, то они ортогональны.
Важно отметить, что ортогональные векторы могут использоваться в различных областях, например, в физике, компьютерной графике и машинном обучении. Знание и умение проверять ортогональность векторов является полезным навыком для работы с линейной алгеброй.
Скалярное произведение векторов: определение и вычисление

Для двух векторов a и b, скалярное произведение обозначается как a · b или a * b. Оно вычисляется по следующей формуле:
a · b = |a| * |b| * cos(θ)
где |a| и |b| - длины векторов a и b соответственно, а θ - угол между ними, измеренный в радианах или градусах.
Вычисление скалярного произведения векторов может быть осуществлено с использованием формулы или расширенной формулы для вычисления косинуса угла между векторами, в зависимости от выбранного способа.
Скалярное произведение векторов имеет несколько полезных свойств. Например, оно позволяет определить, являются ли векторы ортогональными (перпендикулярными) друг другу. Если скалярное произведение двух векторов равно нулю, то они ортогональны. Это полезное свойство может быть использовано для проверки ортогональности векторов.
Скалярное произведение векторов находит применение во многих областях, включая физику, геометрию, компьютерную графику, машинное обучение и др. Оно позволяет измерять сходство или различие между векторами и использовать это в решении различных задач.
Векторное произведение векторов: определение и вычисление

Для вычисления векторного произведения двух векторов необходимо учитывать их направление и длину. Если у векторов есть координаты, то формула для вычисления векторного произведения выглядит следующим образом:
- Пусть вектор A имеет координаты (Ax, Ay, Az), а вектор B – (Bx, By, Bz).
- Тогда векторное произведение A и B, обозначаемое A × B, рассчитывается по формуле:
A × B = (AyBz - AzBy, AzBx - AxBz, AxBy - AyBx)
Результатом вычисления будет трехкомпонентный вектор со значениями по осям x, y и z.
Векторное произведение векторов имеет следующие свойства:
- Если векторы A и B коллинеарны (лежат на одной прямой), то их векторное произведение равно нулевому вектору: A × B = 0.
- Векторное произведение A × B перпендикулярно обоим исходным векторам, то есть оно ортогонально им.
- Модуль векторного произведения равен площади параллелограмма, образованного векторами A и B.
Векторное произведение векторов используется во многих областях науки и техники, таких как физика, геометрия, графика и компьютерная графика. Применимость этой операции позволяет решать различные задачи, связанные с пространственными векторами и плоскостями.
Геометрическая интерпретация ортогональности векторов
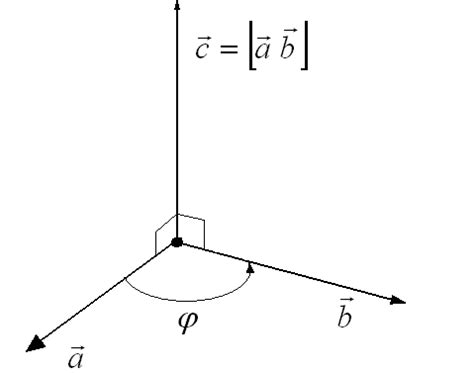
Для понимания геометрической интерпретации ортогональности, необходимо представить два вектора в виде геометрических отрезков на плоскости или в пространстве. Если эти два отрезка пересекаются под прямым углом без смещения, то они являются ортогональными.
Например, рассмотрим два вектора A = (2, 0) и B = (0, -3). Если нарисовать их на координатной плоскости, то можно увидеть, что они перпендикулярны друг другу, образуя прямой угол. Вектор A направлен вдоль положительной оси x, а вектор B вдоль отрицательной оси y. Их поперечное произведение равно 0, что говорит об их ортогональности.
Геометрическая интерпретация ортогональности векторов часто используется во многих областях науки и техники. Например, в физике ортогональные векторы могут представлять силы, направленные в противоположные стороны, или направления движения тела под прямым углом друг к другу.
Также геометрическая интерпретация помогает легко визуализировать и понять свойства ортогональности, такие как коммутативность (свойство перестановки ортогональных векторов) и дистрибутивность (свойство суммы и разности ортогональных векторов).
Примеры ортогональности векторов в различных областях

Векторы, ортогональные друг другу, встречаются во многих областях науки и техники. Рассмотрим несколько примеров:
1. Геометрия:
В пространстве геометрии ортогональные векторы имеют особое значение. Например, векторы, описывающие орты осей координат, являются ортогональными. Это свойство позволяет использовать ортогональность векторов для решения различных задач, связанных с расчетами и построениями в трехмерном пространстве.
2. Физика:
В физике концепция ортогональности векторов широко используется для описания физических явлений. Например, векторы электрического и магнитного полей в курсе электромагнетизма ортогональны друг другу. Это свойство позволяет упростить расчеты и анализ электромагнитных полей.
3. Криптография:
Ортогональные векторы используются в криптографии для создания надежных шифров. Криптографический протокол, основанный на ортогональности векторов, позволяет при передаче информации обеспечить высокую степень надежности и защиты от несанкционированного доступа.
4. Машинное обучение:
Векторы, ортогональные друг другу, также используются в алгоритмах машинного обучения. Например, в методе главных компонент (PCA) ортогональные векторы применяются для снижения размерности данных и удаления коррелированных признаков.
Ортогональность векторов имеет широкий спектр применений и является важным понятием в различных научных и инженерных дисциплинах. Понимание и использование ортогональности векторов позволяет значительно упростить решение задач и улучшить качество результатов во многих областях.



