Уравнения – это математические выражения, которые содержат неизвестные значения, называемые переменными. Обычно уравнения решаются для определенных значений переменных, но иногда возникают ситуации, когда уравнение имеет бесконечное множество корней. Это означает, что любое значение переменной является решением уравнения.
Существует несколько случаев, когда уравнение может иметь бесконечное множество корней. Один из них – это тождественные уравнения, когда обе части уравнения равны друг другу вне зависимости от значений переменных. Например, уравнение 0 = 0 является тождественным и имеет бесконечное множество корней.
Еще один случай – это уравнения, которые охватывают всю числовую ось, такие как уравнение вида x = c, где c является постоянным числом. Независимо от значения переменной x, это уравнение всегда будет истинным, поэтому имеет бесконечное множество корней.
Интересный случай возникает при работе с тригонометрическими уравнениями. Некоторые тригонометрические функции имеют периодическую природу, то есть повторяются через определенные интервалы. Если уравнение содержит периодическую функцию и равенство выполняется для всех значений переменной в этом периоде, то уравнение имеет бесконечное множество корней.
Ситуации, в которых возникает бесконечное множество корней
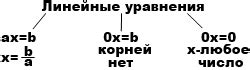
В математике существуют ситуации, когда уравнение может иметь бесконечное множество корней. Это происходит в случае, когда исходное уравнение имеет бесконечное количество решений.
Примером такого уравнения может служить уравнение вида x^2 = 4. Оно имеет два корня: x = 2 и x = -2. Однако, если мы возведем оба этих корня в квадрат, то получим снова 4. Таким образом, в этом уравнении присутствует бесконечное множество решений, так как мы можем брать любое число и возводить его в квадрат, получая при этом значение 4.
Еще одним примером является уравнение вида sin(x) = 0. В этом случае корнями будут все значения аргумента x, при которых sin(x) равно 0. Известно, что это происходит, когда аргумент равен кратному числу π. Таким образом, уравнение имеет бесконечное множество корней: x = nπ, где n - любое целое число.
Такие ситуации возникают, когда уравнение содержит параметры или переменные, которые могут принимать бесконечное количество значений. В таких случаях уравнение может иметь множество корней, которое бесконечно расширяется и не может быть перечислено или ограничено определенным числом.
Изучение уравнений с бесконечным множеством корней имеет важное значение в математике, физике и других науках. Это позволяет рассмотреть различные ситуации, в которых значения переменных могут варьироваться в широком диапазоне.
Уравнения с обратными функциями
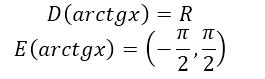
Один из примеров уравнения с обратной функцией – это уравнение синуса:
sin(x) = a
где a – заданное значение между -1 и 1, а x – неизвестная переменная, находящаяся в аргументе обратной функции.
В этом уравнении есть бесконечное множество корней, так как функция синуса повторяется через каждые 2π радиан. То есть, если одно значение x является корнем, то и любое число вида x + 2πn также будет корнем, где n – целое число.
Уравнения с обратными функциями встречаются в различных областях математики и физики, и их решение требует использования специальных методов, таких как графический метод, метод подстановки или использование тригонометрических тождеств.
Такие уравнения могут иметь множество прикладных применений, например, при расчете периодических процессов или моделировании колебательных систем. Поэтому понимание и решение уравнений с обратными функциями является важным элементом изучения математики и науки о природе.
Уравнения с радикалами и их корнями

Одним из примеров уравнений с радикалами является квадратное уравнение с двумя радикалами.
Пример:
$$\sqrt{x+1} + \sqrt{x-3} = 2$$
Для решения такого уравнения нужно выполнить несколько шагов:
1. Избавиться от знаков корней, возвести обе части уравнения в квадрат:
$$(\sqrt{x+1} + \sqrt{x-3})^2 = 2^2$$
2. Раскрыть скобки и привести подобные слагаемые:
$$x+1 + 2\sqrt{(x+1)(x-3)} + x-3 = 4$$
$$2x - 1 + 2\sqrt{x^2 - 2x - 3} = 4$$
3. Перенести все слагаемые в одну часть уравнения:
$$2\sqrt{x^2 - 2x - 3} = 5 - 2x$$
4. Возвести обе части уравнения в квадрат еще раз:
$$(2\sqrt{x^2 - 2x - 3})^2 = (5 - 2x)^2$$
$$4(x^2 - 2x - 3) = 25 - 20x + 4x^2$$
5. Раскрыть скобки, привести подобные слагаемые и привести уравнение к стандартному виду:
$$4x^2 - 8x - 12 = 25 - 20x + 4x^2$$
$$16x = 37$$
6. Найти корни уравнения:
$$x = \frac{37}{16}$$
Таким образом, уравнение $$\sqrt{x+1} + \sqrt{x-3} = 2$$ имеет один корень: $$x = \frac{37}{16}$$.
Решение уравнений с радикалами требует точности и проверки полученного результата. Некоторые уравнения могут иметь дополнительные корни, которые необходимо найти и проверить.
Уравнения, содержащие абсолютные значения

Общий вид уравнений с абсолютными значениями имеет вид:
|x - a| = b |
где x - переменная, a и b - константы, а "|" - символ модуля.
Уравнения такого вида могут иметь как одно, так и бесконечное множество корней. Количество корней зависит от соотношения между значениями a и b.
Решение уравнений с абсолютными значениями можно провести по следующему алгоритму:
- Разбить уравнение на две части, учитывая знак равенства
- Рассмотреть два случая: когда функция модуля больше или равна нулю, и когда она меньше нуля, при этом учесть знак аргумента модуля
- В обоих случаях записать и решить систему уравнений
- Полученные корни проверить и выбрать только те, которые удовлетворяют исходному уравнению
Результатом решения уравнения с абсолютными значениями могут быть как конкретные числа, так и интервалы или условия в виде неравенств.
Знание методики решения уравнений с абсолютными значениями позволяет более гибко анализировать и строить модели, основанные на подобных уравнениях. Такие уравнения активно применяются в физике и экономике для моделирования различных процессов и явлений.
Признаки бесконечного множества корней в квадратных уравнениях
Нормально, квадратное уравнение имеет два корня. Однако, иногда оно может иметь бесконечное множество корней. Признаки бесконечного множества корней в квадратных уравнениях могут быть следующими:
- Когда коэффициент a равен нулю. В этом случае уравнение преобразуется в линейное уравнение bx + c = 0, где b ≠ 0. Линейное уравнение имеет только одно решение.
- Когда коэффициенты a, b и c равны нулю. В этом случае уравнение преобразуется в тождественное уравнение 0 = 0, которое верно для всех значений x. Таким образом, уравнение имеет бесконечное множество корней.
- Когда коэффициенты a и c равны нулю, а коэффициент b ≠ 0. В этом случае уравнение преобразуется в линейное уравнение bx = 0, которое также имеет бесконечное множество корней.
Важно отметить, что признаки бесконечного множества корней в квадратных уравнениях допустимы только в случае, когда выполняются указанные условия. В остальных случаях уравнение будет иметь два различных корня или не иметь корней вовсе.
Многочлены с одинаковыми корнями и их свойства

Одним из интересных случаев является ситуация, когда у разных многочленов имеются одинаковые корни. Это означает, что разные многочлены могут описывать одну и ту же зависимость между переменными.
Многочлены с одинаковыми корнями обладают несколькими интересными свойствами. Во-первых, если два многочлена имеют одинаковый корень, то их разность (вычитание одного многочлена из другого) будет иметь этот же корень. Иными словами, если x – корень многочлена P(x), то он будет являться корнем также и для многочлена P(x) - Q(x).
Во-вторых, если два многочлена имеют одинаковые корни, то их произведение будет иметь те же корни. То есть, если x – корень многочлена P(x), то он будет являться корнем также и для многочлена P(x) * Q(x).
Также стоит отметить, что если многочлен имеет корень кратности больше 1, то он будет также иметь все корни, являющиеся этим же числом.
Многочлены с одинаковыми корнями – это интересный объект изучения в алгебре, который находит применение в различных областях математики и естествознания.
| Свойство | Описание |
|---|---|
| Разность многочленов | Если два многочлена имеют одинаковый корень, то их разность будет иметь этот же корень. |
| Произведение многочленов | Если два многочлена имеют одинаковые корни, то их произведение будет иметь те же корни. |
| Кратность корня | Если многочлен имеет корень кратности больше 1, то он будет также иметь все корни, являющиеся этим же числом. |
Системы уравнений с бесконечным множеством решений

В математике существуют системы уравнений, которые имеют бесконечное множество решений. Это означает, что существует бесконечное количество значений переменных, которые удовлетворяют данным уравнениям.
Такие системы уравнений могут возникать в различных случаях. Например, когда в системе уравнений присутствует переменная, которая не ограничена никакими условиями и может принимать любые значения.
Одним из примеров системы уравнений с бесконечным множеством решений является система линейных уравнений, в которой есть лишь одно уравнение с большим количеством неизвестных. В таком случае, каждая переменная может принимать любое значение, что приводит к бесконечности решений.
Системы уравнений с бесконечным множеством решений могут иметь различные приложения в реальных задачах. Например, они могут быть использованы для описания физических законов или состояний систем, где переменные могут принимать широкий спектр значений.
Исследование систем уравнений с бесконечным множеством решений является одной из важных областей математики. Оно помогает уточнить понятие о решении уравнений, а также найти различные способы описания бесконечного множества решений.
Границы бесконечного множества корней в трансцендентных уравнениях
Рассмотрим трансцендентное уравнение вида:
$$f(x) = 0,$$
где $f(x)$ - трансцендентная функция, зависящая от переменной $x$. Бесконечное множество корней возникает в случае, если существует последовательность значений $x_n$, стремящихся к бесконечности, такая что $f(x_n) = 0$ для всех $n$.
Также, границы бесконечного множества корней можно определить, исходя из особенностей графика функции $f(x)$. Например, если функция имеет бесконечное число пересечений с осью абсцисс, то уравнение будет иметь бесконечное множество корней.
Интересно отметить, что трансцендентные уравнения с бесконечным множеством корней имеют важное значение в различных областях науки и техники. Они часто возникают в задачах оптимизации, моделировании и анализе сложных систем.



