Разложение функции в ряд Тейлора является очень полезным инструментом в математическом анализе. Оно позволяет аппроксимировать сложные функции более простыми и понятными способами. Однако, перед тем как применять разложение в ряд Тейлора, необходимо удостовериться в его применимости. В этой статье мы рассмотрим некоторые критерии, которые помогут определить, когда можно использовать разложение в ряд Тейлора для данной функции.
Первый критерий - функция должна быть бесконечно дифференцируемой в заданной точке. Это значит, что все ее производные должны существовать и быть непрерывными в окрестности этой точки. Если функция имеет точку разрыва или несуществует некоторая производная в заданной точке, то разложение в ряд Тейлора для этой функции не применимо.
Второй критерий - функция должна иметь непрерывные производные всех порядков в заданной окрестности точки разложения. Если производные функции имеют разрывы или несуществуют в некоторых точках окрестности, то разложение в ряд Тейлора может дать неточные результаты.
Третий критерий - разложение в ряд Тейлора работает лучше для функций, чья окрестность разложения не слишком широкая. Если окрестность разложения слишком большая, то разложение в ряд Тейлора может давать неточные результаты и не являться эффективным методом аппроксимации функции.
Ознакомившись с этими критериями, каждый математик сможет определить, когда применимо разложение в ряд Тейлора для изучаемой им функции. Этот метод позволяет упростить анализ сложных функций и получить приближенные значения для определения их свойств и поведения в окрестности заданной точки. Важно помнить, что применение разложения в ряд Тейлора следует комбинировать с другими методами анализа, чтобы получить более полную картину и более точные результаты.
Критерии применимости разложения

1. Функция должна быть достаточно гладкой. Разложение в ряд Тейлора применимо только к функциям, имеющим непрерывные производные всех порядков в рассматриваемой точке. Если функция имеет разрывы или не является гладкой в данной точке, то разложение в ряд Тейлора может быть неточным или даже неприменимым.
2. Точка разложения должна быть достаточно близко к целевой точке. Чем ближе точка разложения к целевой точке, тем точнее будет разложение в ряд Тейлора. Если точка разложения находится достаточно далеко от целевой точки, то возможны значительные погрешности в результате аппроксимации.
3. Ряд должен сходиться к исходной функции. Разложение в ряд Тейлора является аппроксимацией функции с использованием ее производных в заданной точке. Для того, чтобы разложение было точным, ряд должен сходиться к исходной функции в окрестности точки разложения. Если ряд не сходится или сходится медленно, то разложение в ряд Тейлора может быть неприменимо или дающим неточные результаты.
4. Условия окружающей среды должны быть учтены. Разложение в ряд Тейлора предполагает, что окружающая среда и условия эксперимента остаются неизменными. Если окружающая среда или условия эксперимента изменяются, то результаты разложения могут быть неточными или неприменимыми.
5. Учет остаточного члена. Разложение в ряд Тейлора даёт аппроксимацию заданной функции с некоторой погрешностью. Остаточный член, который не учитывается в аппроксимации, может оказывать существенное влияние на точность разложения. Поэтому при применении разложения в ряд Тейлора необходимо учитывать остаточный член и его влияние на точность результатов.
- Используйте разложение в ряд Тейлора с осторожностью, учитывая заявленные критерии применимости.
- Проверяйте точность разложения и учитывайте остаточный член для получения более точных результатов.
- Обратитесь к математической литературе или консультантам для получения дополнительной информации о применимости разложения в ряд Тейлора в вашем конкретном случае.
Разложение в ряд Тейлора

Разложение в ряд Тейлора особенно полезно в случаях, когда аналитическое выражение функции сложно или неизвестно, но известны значения функции и ее производных в некоторой точке. В таких случаях разложение в ряд Тейлора позволяет приближенно предсказать значения функции в других точках.
Степень аппроксимации зависит от числа членов ряда, используемых для приближения функции. Чем больше членов ряда мы используем, тем точнее будет приближение. Однако по мере увеличения числа членов ряда могут возникать сложности с вычислениями, поэтому в практических расчетах обычно используют конечное число членов.
Разложение в ряд Тейлора может быть применено к широкому классу функций, но есть некоторые условия, которые должны быть выполнены для успешного применения этого метода. Во-первых, функция должна быть дифференцируемой бесконечное число раз в заданной точке. Кроме того, радиус сходимости ряда может быть ограничен, и в некоторых случаях разложение может быть плохо аппроксимирующим.
Важно помнить, что разложение в ряд Тейлора является приближенным представлением функции и может быть использовано только в определенных условиях применимости.
Определение разложения в ряд Тейлора

Разложение в ряд Тейлора определяется формулой:
f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)(x-a)^2}{2!} + \frac{f'''(a)(x-a)^3}{3!} + \cdots
где f(x) - исходная функция, f(a) - значение функции в точке a, f'(a) - первая производная функции в точке a, f''(a) - вторая производная функции в точке a и т.д.
Разложение в ряд Тейлора позволяет аппроксимировать функцию в окрестности точки a с заданной точностью. Чем больше слагаемых участвует в разложении, тем точнее аппроксимация.
Разложение в ряд Тейлора используется во многих областях науки и техники, например, в физике, экономике, компьютерной графике и других. Оно позволяет упростить сложные функции и упрощает решение уравнений.
Необходимые условия для применимости

| Условие | Описание |
|---|---|
| Функция должна быть бесконечно дифференцируемой | Чтобы разложение в ряд Тейлора имело смысл, функция должна иметь бесконечное количество производных в окрестности точки разложения. Это означает, что функция должна быть бесконечно дифференцируемой в данной окрестности. |
| Интервал сходимости должен содержать точку разложения | Интервал сходимости разложения в ряд Тейлора должен содержать точку разложения. Интервал сходимости определяет, в какой области значения функции сходятся к разложению в ряд Тейлора. Если точка разложения выходит за пределы интервала сходимости, то разложение не будет справедливым. |
| Ряд должен сходиться к функции в окрестности точки разложения | Ряд Тейлора должен сходиться к исходной функции в окрестности точки разложения. Это означает, что сумма ряда должна стремиться к функции при увеличении числа слагаемых. Если ряд не сходится к функции, то его использование для аппроксимации функции будет неоправданным. |
Все эти условия являются необходимыми, но не достаточными для применимости разложения в ряд Тейлора. Дополнительно могут возникать другие ограничения, такие как ограничение на длину интервала сходимости или ограничение на значение аргумента функции. Поэтому перед применением разложения в ряд Тейлора необходимо провести анализ и проверить выполнение всех условий.
Ограниченность функции и ее производных
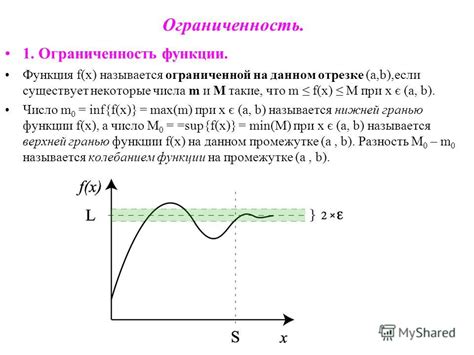
Функция называется ограниченной на интервале, если у нее существует такое число M, что для любого значения x из этого интервала выполняется неравенство |f(x)| ≤ M. Если функция ограничена на всей числовой оси, то она называется ограниченной функцией.
Ограниченность функции является важной характеристикой для применимости разложения в ряд Тейлора. Если функция не является ограниченной, то ряд Тейлора может не сходиться к исходной функции. Это связано с тем, что ряд Тейлора использует значения производных функции в окрестности точки разложения, и если эти производные не ограничены, то можно получить расходимость ряда.
Кроме ограниченности самой функции, важна также ограниченность всех ее производных на интервале, на котором рассматривается разложение. Если производные функции ограничены на данном интервале, то разложение в ряд Тейлора является справедливым.
Следовательно, при изучении применимости разложения в ряд Тейлора необходимо учитывать ограниченность самой функции и всех ее производных. Только в случае выполнения этих условий можем говорить о применимости разложения в ряд Тейлора и его адекватности для приближения функции на заданном интервале.
Точка разложения

Точка разложения - это точка, вокруг которой происходит разложение функции в ряд Тейлора. Выбор точки разложения влияет на сходимость и точность разложения.
Идеальная точка разложения находится вблизи значения, для которого требуется произвести аппроксимацию. Чем ближе точка разложения к значению, тем точнее будет разложение.
Особое внимание следует уделять точке разложения, если функция имеет особенности или расхождения в окрестности определенной точки. В таких случаях разложение в ряд Тейлора может быть неприменимо и требуется использовать другие методы аппроксимации.
Критерий равномерной сходимости ряда Тейлора

Ряд Тейлора сходится равномерно в заданной области, если для любого числа ε>0 найдется такое натуральное число N, что для всех x из области и для любого натурального числа n>N выполняется неравенство |Rn(x)| n(x) - остаточный член ряда Тейлора для функции в точке x.
Таким образом, критерий равномерной сходимости ряда Тейлора заключается в том, что остаточные члены ряда должны стремиться к нулю равномерно по всей области сходимости. Это позволяет использовать ряд Тейлора для получения приближенных значений функции с произвольной точностью.
Точность приближения с использованием ряда Тейлора

Для того чтобы оценить точность приближения с использованием ряда Тейлора, необходимо учесть несколько важных критериев. Во-первых, необходимо принять во внимание, что ряд Тейлора является приближением, а не точной формулой. Точность приближения будет зависеть от степени разложения ряда и удаленности от центральной точки разложения.
Во-вторых, точность приближения будет зависеть от поведения функции в окрестности точки разложения. Если функция сильно меняется или имеет особенности, то ряд Тейлора может быть плохим приближением. В таких случаях необходимо учиться выбирать правильную точку разложения для достижения максимальной точности.
Также важно учитывать остаточный член ряда Тейлора, который показывает неравенство между исходной функцией и ее приближением. Чем меньше остаточный член, тем точнее приближение с использованием ряда Тейлора.
Наконец, точность приближения можно улучшить, увеличивая степень разложения ряда Тейлора. Однако следует помнить, что с увеличением степени разложения может возрастать сложность вычислений и увеличиваться погрешность при работе с округлением.
Примеры применения разложения в ряд Тейлора

1. Вычисление синуса:
Разложение функции синуса в ряд Тейлора позволяет приближенно вычислить значение синуса для любого угла. Например, используя разложение синуса в окрестности точки 0, мы можем приближенно вычислить синус 30 градусов. Разложение синуса имеет вид:
sin(x) ≈ x - x^3/3! + x^5/5! - x^7/7! + ...
2. Приближенное вычисление функций:
Разложение функций в ряд Тейлора позволяет приближенно вычислять значения функций вблизи заданной точки. Например, разложение функции e^x позволяет приближенно вычислить значение экспоненты для любого значения аргумента. Разложение для e^x имеет вид:
e^x ≈ 1 + x + x^2/2! + x^3/3! + ...
3. Определение асимптотического поведения функции:
Разложение в ряд Тейлора может использоваться для определения асимптотического поведения функции в окрестности заданной точки. Например, разложение функции ln(x) в окрестности точки 1 позволяет определить поведение функции вблизи этой точки. Разложение ln(x) имеет вид:
ln(x) ≈ (x - 1) - (x - 1)^2/2 + (x - 1)^3/3 - ...
Это помогает понять, как функция ведет себя при стремлении аргумента к 1.
Таким образом, разложение в ряд Тейлора является мощным инструментом, который находит применение в различных областях математики и физики, позволяя приближенно вычислять значения сложных функций и анализировать их поведение вблизи заданной точки.



