Смешанное произведение векторов - это математическая операция, которая используется в линейной алгебре и геометрии. Его также называют смешанное тройное произведение. Смешанное произведение трех векторов равно нулю, если эти векторы лежат в одной плоскости. В противном случае, смешанное произведение не равно нулю и является полезным инструментом в решении различных задач и проблем.
Смешанное произведение векторов может быть положительным, отрицательным или нулевым. Если смешанное произведение равно нулю, то это означает, что объемный параллелепипед, образованный этими векторами, имеет нулевой объем. Это означает, что векторы лежат в одной плоскости и их ориентации можно установить с помощью правила правой руки.
Смешанное произведение векторов широко используется в физике, геометрии и механике. Оно позволяет определить площадь треугольника или объем параллелепипеда. Кроме того, смешанное произведение используется для нахождения углов и расстояний между векторами, а также для решения задач с вращением и движением тел.
Векторное произведение и его свойства

Свойства векторного произведения:
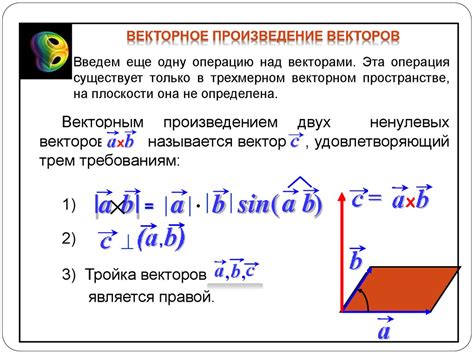
- Векторное произведение двух векторов всегда перпендикулярно плоскости, в которой лежат исходные векторы.
- Модуль векторного произведения равен произведению модулей умножаемых векторов и синуса угла между ними.
- Если векторное произведение равно нулю, то исходные векторы либо коллинеарны, либо один из них нулевой.
- Векторное произведение обладает антикоммутативным свойством, то есть изменение порядка векторов приводит к изменению направления результатирующего вектора.
- Векторное произведение можно представить в виде определителя третьего порядка, составленного из компонент векторов.
Векторное произведение находит свое применение в геометрии, физике, механике и других областях науки. Оно используется, например, для определения момента силы, решения систем уравнений и вычисления площади треугольника. Изучение свойств векторного произведения позволяет более глубоко понять его природу и применение в различных задачах.
Математическое определение и свойства векторного произведения

Математическое определение векторного произведения векторов a и b выглядит следующим образом:
c = a × b
где c - это новый вектор, полученный в результате векторного произведения a и b.
Основным свойством векторного произведения является то, что направление полученного вектора перпендикулярно плоскости, образованной векторами a и b, а его модуль равен площади параллелограмма, построенного на этих векторах.
Также векторное произведение обладает следующими свойствами:
- Антикоммутативность: векторное произведение меняет знак при изменении порядка векторов, то есть a × b = -b × a.
- Дистрибутивность относительно сложения: (a + b) × c = a × c + b × c.
- Ассоциативность относительно умножения на скаляр: (λa) × b = a × (λb) = λ(a × b), где λ - произвольный скаляр.
Векторное произведение имеет широкое применение в различных областях науки и техники, включая физику, геометрию, механику и электротехнику. Оно позволяет решать задачи, связанные с вычислением момента силы, определением направления магнитного поля и другими задачами, требующими учета векторных характеристик.
Условия, при которых векторное произведение равно 0
| Условие | Описание |
|---|---|
| Вектора коллинеарны | Если исходные вектора коллинеарны, то их векторное произведение равно 0. Коллинеарные векторы лежат на одной прямой. |
| Один из векторов нулевой | Если один из исходных векторов является нулевым вектором, то его векторное произведение с любым другим вектором будет равно 0. |
| Вектора компланарны | Если исходные вектора лежат в одной плоскости, то их векторное произведение будет равно 0. Компланарные вектора образуют плоскость. |
Условия, при которых векторное произведение равно 0, имеют важное значение в математике и физике. Знание этих условий позволяет более глубоко разобраться в свойствах векторного анализа и его применении в различных областях науки.
Геометрическая интерпретация смешанного произведения векторов
Смешанное произведение трех векторов a, b и c равно 0 тогда и только тогда, когда векторы a, b и c являются коллинеарными или компланарными.
Если смешанное произведение равно 0, то это означает, что объем параллелепипеда, образованного векторами a, b и c, равен 0. Таким образом, векторы a, b и c лежат на одной плоскости или прямой.
Геометрическая интерпретация смешанного произведения векторов может быть использована для решения различных геометрических задач. Например, если нам даны три вектора a, b и c и смешанное произведение равно 0, то мы можем заключить, что эти векторы лежат на одной плоскости и могут использоваться для построения треугольника или для нахождения площади этой плоскости.
Также смешанное произведение векторов может быть использовано для определения ориентации плоскости или объема фигуры, образованной векторами. Если смешанное произведение положительное, то объем или площадь положительны, а если смешанное произведение отрицательное, то объем или площадь отрицательны.
Таким образом, геометрическая интерпретация смешанного произведения векторов является мощным инструментом для анализа геометрических задач и может быть полезна в различных областях, таких как геометрия, физика и компьютерная графика.
Практические примеры использования смешанного произведения векторов

- Вычисление объема параллелепипеда: Смешанное произведение векторов позволяет вычислить объем параллелепипеда, построенного на этих векторах. Для этого необходимо взять три вектора, составляющих ребра параллелепипеда, и вычислить их смешанное произведение. Модуль этого смешанного произведения будет равен объему параллелепипеда.
- Определение коллинеарности векторов: Смешанное произведение векторов может использоваться для определения коллинеарности трех векторов. Если смешанное произведение векторов равно нулю, то векторы являются коллинеарными, то есть лежат на одной прямой.
- Вычисление площади треугольника: Смешанное произведение векторов может быть использовано для вычисления площади треугольника. Для этого необходимо взять два вектора, которые являются сторонами треугольника, и вычислить половину модуля смешанного произведения этих векторов.
- Нахождение нормали к плоскости: Нормаль к плоскости может быть найдена с помощью смешанного произведения векторов, лежащих на этой плоскости. Для этого необходимо взять два ненулевых вектора, лежащих на плоскости, и вычислить их смешанное произведение. Нормаль к плоскости будет перпендикулярна этому смешанному произведению.
- Решение систем линейных уравнений: Смешанное произведение векторов может быть использовано для решения систем линейных уравнений. Если в системе имеется три уравнения с тремя неизвестными и смешанное произведение векторов, составленных из коэффициентов при неизвестных, равно нулю, то система имеет решение.
Таким образом, смешанное произведение векторов является мощным инструментом, который находит применение в различных задачах и областях математики и физики.



