Окружность, которая вписана в многоугольник, является интересным геометрическим объектом, который находит свое применение в различных областях науки и техники. В сущности, вписанная окружность представляет собой окружность, которая касается всех сторон многоугольника и находится внутри его.
Одно из основных свойств вписанной окружности заключается в том, что ее центр совпадает с центром многоугольника. Это означает, что все радиусы окружности равны друг другу и равны расстоянию от центра окружности до любой стороны многоугольника.
Самой заметной особенностью окружности, вписанной в многоугольник, является то, что она делит каждую сторону многоугольника на две взаимно пропорциональные отрезки. То есть, отрезки, которые соединяют вершины многоугольника с точками касания окружности, делятся в одном и том же отношении.
Примеры многоугольников, в которых можно найти вписанную окружность, включают такие фигуры, как треугольник, четырехугольник, пятиугольник и т.д. Многоугольник должен быть выпуклым, то есть все его углы должны быть меньше 180 градусов. Также вписанная окружность существует только в многоугольниках с нечетным числом сторон, например, в пятиугольнике или семиугольнике.
Определение окружности, вписанной в многоугольник
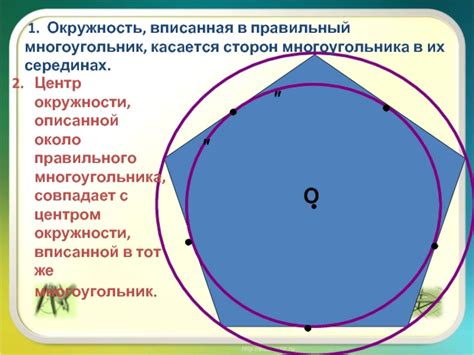
Другими словами, вписанная окружность является окружностью, центр которой совпадает с центром многоугольника, а радиус равен расстоянию от центра многоугольника до одной из его сторон.
Особенное свойство вписанной окружности заключается в том, что она проходит через вершины многоугольника и касается каждой его стороны в одной точке. Это свойство позволяет связать радиус вписанной окружности с длинами сторон многоугольника.
Окружность, вписанная в треугольник, называется вписанной окружностью треугольника. Аналогично, вписанная окружность пятиугольника называется вписанной окружностью пятиугольника, и так далее.
 | На рисунке показан пример окружности, вписанной в многоугольник. Красный круг обозначает вписанную окружность, а стороны многоугольника являются хордами этой окружности. |
Определение многоугольника
Многоугольники классифицируются по количеству и форме сторон. Если все стороны многоугольника равны, то такой многоугольник называется равносторонним. Если все углы многоугольника равны, то такой многоугольник называется равноугольным. Если же все стороны и углы многоугольника равны, то он называется правильным.
Многоугольник может иметь различное количество сторон - от треугольника (три стороны) до n-угольника (n сторон). В зависимости от количества сторон, многоугольник может иметь различные названия: треугольник, четырехугольник (квадрат, прямоугольник, ромб, параллелограмм), пятиугольник (пятиконечная звезда), шестиугольник (шестиугольная звезда), и так далее.
Многоугольники могут быть выпуклыми или невыпуклыми. Если все углы многоугольника выпуклы (меньше 180 градусов), то он является выпуклым. В противном случае, если углы многоугольника невыпуклы (больше 180 градусов), то он является невыпуклым.
| Количество сторон | Название |
|---|---|
| 3 | Треугольник |
| 4 | Четырехугольник (квадрат, прямоугольник, ромб, параллелограмм) |
| 5 | Пятиугольник (пятиконечная звезда) |
| 6 | Шестиугольник (шестиугольная звезда) |
| n | n-угольник |
Определение окружности

Окружность обладает следующими основными свойствами:
- Диаметр окружности - это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
- Радиус окружности - это отрезок, соединяющий центр окружности с любой точкой на окружности.
- Длина окружности - это периметр окружности и может быть вычислена с помощью формулы L = 2πr, где L - длина окружности, π (пи) - математическая постоянная, приближенное значение которой равно 3.14, r - радиус окружности.
- Площадь окружности - это площадь закрашенной области внутри окружности и может быть вычислена с помощью формулы S = πr^2, где S - площадь окружности, π (пи) - математическая постоянная, приближенное значение которой равно 3.14, r - радиус окружности.
Окружность выделяется своей симметричностью и равноудаленностью всех ее точек от центра. Окружность часто используется в геометрии и в других областях науки и техники. Она является основой для понимания и решения задач, связанных с геометрическими построениями и измерениями.
Определение вписанной окружности

Для того чтобы вписанная окружность существовала, необходимо, чтобы количество сторон многоугольника было не менее трех.
Доказательство того, что окружность действительно вписана в многоугольник, заключается в том, что каждая сторона многоугольника является касательной к окружности. Касательная к окружности в точке касания перпендикулярна радиусу окружности.
Вписанная окружность обладает рядом интересных свойств. Например, радиус вписанной окружности является перпендикуляром к соответствующей стороне многоугольника и проходит через ее середину. Длина каждого отрезка радиуса, проведенного от центра вписанной окружности до точки касания, одинакова. Также, для многоугольника, вписанного в окружность, сумма всех углов при его вершинах равна 360 градусов.
Свойства окружности, вписанной в многоугольник
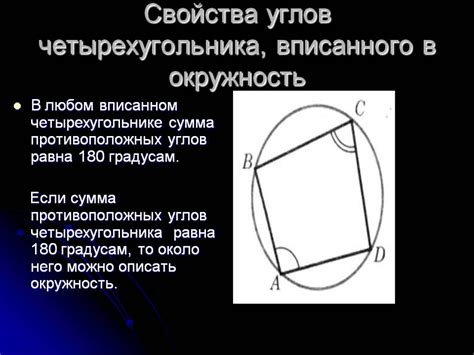
Окружность, вписанная в многоугольник, обладает несколькими интересными свойствами, которые можно использовать для решения геометрических задач.
1. Точка касания: Вписанная окружность касается каждой стороны многоугольника в одной точке. Эта точка называется точкой касания. Она является вершиной прямоугольника, образованного секущими линиями, проведенными из центра окружности до точек касания.
2. Перпендикулярность: Линия, проведенная из центра окружности до точки касания, является перпендикуляром к соответствующей стороне многоугольника. Это означает, что угол между этой стороной и линией, проведенной из центра окружности, равен 90 градусов.
3. Смежные углы: Две стороны многоугольника, соприкасающиеся с одной и той же точкой касания, образуют смежные углы. Эти углы имеют одинаковую величину и равны половине центрального угла многоугольника. Другими словами, смежные углы равны половине угла, образованного двумя радиусами, проведенными из центра окружности в смежные точки касания.
4. Центр окружности: Центр вписанной окружности является центром симметрии многоугольника. Это означает, что любая линия, проходящая через центр окружности, также будет проходить через точку пересечения противоположных сторон многоугольника. Кроме того, центр окружности равноудален от всех сторон многоугольника.
| Количество сторон многоугольника (n) | Радиус вписанной окружности (r) | Длина стороны многоугольника (s) | Центральный угол (θ) многоугольника |
|---|---|---|---|
| 3 | r = s / (2 * √3) | s = 2 * r * √3 | θ = 60° |
| 4 | r = s / 2 | s = 2 * r | θ = 90° |
| 5 | r = s / (2 * √5 * (1 + √5)) | s ≈ 1.17557 * r | θ = 108° |
Это лишь некоторые из свойств окружности, вписанной в многоугольник. Изучение этих свойств позволяет решать различные геометрические задачи, связанные с многоугольниками и окружностями.
Свойство радиуса и диаметра окружности
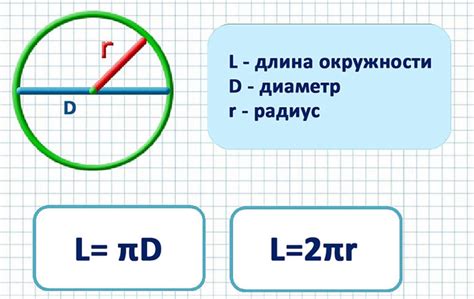
Свойства радиуса:
- Радиус окружности всегда положительный и не может быть отрицательным или равным нулю.
- Длина окружности равна произведению радиуса на двойное значение числа π (примерно 3,14159).
- Радиус является половиной диаметра окружности.
- Радиус окружности также может быть использован для вычисления площади окружности по формуле S = πr2, где S - площадь, радиус r.
Диаметр окружности - это отрезок, проходящий через центр окружности и заканчивающийся на обоих сторонах на окружности. Диаметр обозначается символом d. Диаметр является прямой двух касательных, проходящих через центр окружности.
Свойства диаметра:
- Диаметр является характеристикой окружности и определяет ее размер.
- Диаметр равен удвоенному значению радиуса, то есть d = 2r.
- Длина диаметра равна удвоенной длине радиуса, то есть Ld = 2Lr.
Свойства радиуса и диаметра окружности обеспечивают важные математические зависимости, которые используются при решении различных задач, связанных с окружностями и многоугольниками.
Свойство касательной
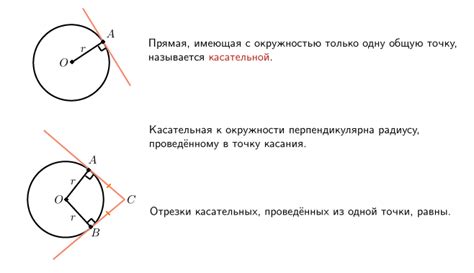
Это свойство можно использовать для вычисления длин сторон многоугольника, если известен радиус вписанной окружности. Для этого нужно провести касательные из вершины многоугольника до окружности и измерить получившиеся отрезки.
Также, зная радиус вписанной окружности и длину одной из сторон многоугольника, можно найти площадь многоугольника по формуле: площадь = полупериметр * радиус, где полупериметр вычисляется как сумма всех сторон многоугольника, деленная на 2.
Свойство касательной позволяет установить взаимосвязь между окружностью и многоугольником и применять его для решения различных геометрических задач.
Свойство хорды
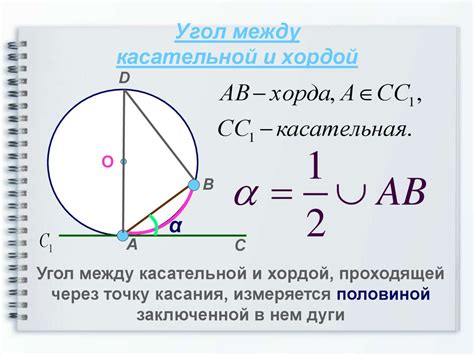
Самое основное свойство хорды заключается в том, что хорда всегда меньше диаметра окружности. Другими словами, длина любой хорды всегда меньше длины диаметра. Это свойство легко проверить на практике: взять любую окружность и провести хорду, затем замерить ее длину и сравнить с длиной диаметра.
Еще одно свойство хорд состоит в том, что хорды, равноудаленные от центра окружности, равны между собой. Если провести хорды AB и CD, такие, что точки A и C равноудалены от центра окружности, то длина хорды AB будет равна длине хорды CD.
Также в вписанном многоугольнике хорды создают равные дуги на окружности. Для любой хорды, проходящей через точки A и B, дуга AB будет равна дуге BA.
Свойства хорд являются основой для решения многих задач, связанных с вписанными многоугольниками. Они позволяют находить длины отрезков, радиусы окружностей и углы в многоугольнике.



