Когда матрица имеет бесконечное множество решений: причины и методы решения

В линейной алгебре существует ситуация, когда система линейных уравнений имеет бесконечное множество решений. Это может произойти, когда матрица системы не полного ранга или содержит свободные переменные. В таких случаях нельзя однозначно определить значения искомых переменных, и требуется применение специальных методов для решения таких систем. В данной статье мы рассмотрим причины возникновения бесконечных множеств решений и методы их нахождения.

Одной из основных причин возникновения бесконечного множества решений является ситуация, когда система линейных уравнений содержит неизвестные, зависящие друг от друга, то есть система содержит свободные переменные. Это означает, что значения свободных переменных можно задавать произвольно, что приводит к бесконечному количеству возможных комбинаций значений и, соответственно, решений системы.

Для решения системы уравнений с бесконечным множеством решений требуется использовать специальные методы. Один из таких методов - метод Гаусса. С его помощью можно привести матрицу системы к улучшенному ступенчатому виду, где можно выделить базисные и свободные переменные. Базисные переменные определяются ненулевыми столбцами улучшенной ступенчатой матрицы, а свободные переменные - нулевыми столбцами. Затем, используя значения свободных переменных, можно получить бесконечное множество решений системы.

Матрица с бесконечным множеством решений

В линейной алгебре матрица с бесконечным множеством решений возникает, когда система уравнений, представленная матрицей и вектором правой части, имеет бесконечное количество решений. Это возможно из-за особенностей структуры или связи между строками и столбцами матрицы.

Одна из главных причин возникновения матрицы с бесконечным множеством решений - наличие линейно зависимых строк или столбцов. Линейная зависимость между строками означает, что одна строка может быть выражена через линейную комбинацию других строк. Аналогично, линейная зависимость между столбцами означает, что один столбец может быть представлен в виде линейной комбинации других столбцов.

В случае, когда порядок матрицы (количество строк) больше, чем количество ненулевых строк, система уравнений, представленная матрицей, будет иметь бесконечное число решений. В этом случае, имеется свобода выбора для определенных переменных, которые могут принимать любые значения. Это можно представить в виде параметрического решения, где каждая переменная связана с параметром.

Для решения системы уравнений с бесконечным множеством решений можно использовать методы Гаусса, Жордана-Гаусса или метод Крамера. Эти методы позволяют найти решение системы уравнений в виде параметрической формы или матричного выражения, и определить значения параметров для получения частного решения.

Причины такого явления

Существует несколько причин, по которым матрица может иметь бесконечное множество решений:

Линейно зависимые строки или столбцы. Если в матрице есть линейно зависимые строки или столбцы, то это означает, что один из них может быть выражен через другие. В таком случае, у матрицы есть бесконечное множество решений, так как можно выбрать любое значение для свободного элемента.
Совпадение двух строк или столбцов. Если в матрице есть две одинаковые строки или столбца, то это означает, что одна строка или столбец может быть выражена через другую. В этом случае, матрица также имеет бесконечное множество решений.
Недостаток информации. Если в матрице не хватает информации для однозначного определения всех неизвестных, то она будет иметь бесконечное множество решений. Например, если в системе уравнений есть больше неизвестных, чем уравнений, или если в матрице присутствуют свободные переменные.

Причины бесконечного множества решений могут быть различными, и для того чтобы решить такую матрицу, требуется применение специальных методов, таких как метод Гаусса или метод Жордана-Гаусса. Эти методы позволяют найти общий вид решения и определить все возможные значения для свободных элементов.

Методы решения системы уравнений

Существует несколько методов решения системы уравнений, когда матрица этой системы имеет бесконечное множество решений. Они могут быть полезны при анализе линейных зависимостей или при построении аналитических моделей.

Один такой метод - метод Гаусса. Он основан на приведении матрицы системы к ступенчатому виду и последующем обратном ходе. Если такой вид будет содержать некоторые элементы, которые равны нулю, то это будет означать наличие бесконечного множества решений.

Еще один метод - метод Крамера. Он основан на вычислении определителей матрицы системы. Если главный определитель равен нулю, то это будет означать наличие бесконечного множества решений.

Также существует метод обратной матрицы, который используется для систем уравнений с квадратной матрицей. Если обратная матрица не существует, то это будет означать наличие бесконечного множества решений.

Выбор конкретного метода будет зависеть от особенностей системы уравнений и предпочтений решателя. Использование этих методов поможет получить полное представление о природе и множестве решений системы уравнений.

Линейно зависимые столбцы матрицы

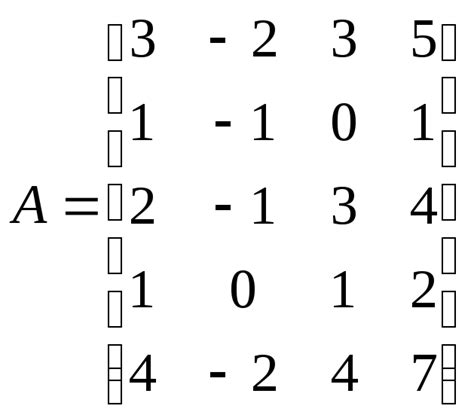
Линейная зависимость столбцов может возникнуть по нескольким причинам. Одна из основных причин - наличие столбца, являющегося линейной комбинацией других столбцов. Такой столбец можно выразить через другие столбцы путем умножения каждого столбца на некоторое число и сложения результатов.

Наличие линейно зависимых столбцов ведет к тому, что матрица имеет бесконечное множество решений или не может быть обратима. Это может означать, что система уравнений, заданная матрицей, имеет бесконечное количество решений или не имеет решений вовсе.

Для определения линейной зависимости столбцов матрицы можно использовать различные методы, такие как метод Гаусса, определители, элементарные преобразования. Одним из самых простых способов является проверка линейной комбинации столбцов на равенство нулевому вектору. Если найдется нетривиальная комбинация, которая равна нулевому вектору, то столбцы линейно зависимы.

Линейно зависимые столбцы матрицы играют важную роль в линейной алгебре и имеют широкое применение в различных областях, таких как физика, экономика, компьютерная графика и другие.

Сингулярность матрицы

Одной из причин сингулярности матрицы может быть неправильное построение матрицы. Например, при наличии линейно зависимых строк или столбцов в матрице, определитель будет равен нулю, что приведет к сингулярности матрицы. Также, сингулярность может возникать при применении некоторых математических операций, которые приводят к потере информации и ухудшению обратимости матрицы.

Для решения систем уравнений, связанных с сингулярной матрицей, существуют различные методы. Одним из них является использование псевдообратной матрицы. Псевдообратная матрица позволяет решить систему уравнений, даже если матрица является сингулярной. Этот метод основан на поиске такой матрицы, которая при умножении на сингулярную матрицу даст единичную матрицу.

Еще одним методом решения системы уравнений с сингулярной матрицей является использование метода Гаусса-Джордана. Этот метод позволяет придти к эквивалентному виду системы, в котором сингулярная матрица становится обратимой. Для этого применяются элементарные преобразования строк и столбцов матрицы.

Важно отметить, что решение системы уравнений с сингулярной матрицей может быть неединственным, поскольку оно зависит от выбора начальных условий и метода решения. Поэтому, при решении систем с сингулярными матрицами необходимо учитывать возможность наличия бесконечного множества решений и проводить дополнительные проверки для определения корректности полученных результатов.

Методы решения системы линейных уравнений

1. Метод Крамера

Метод Крамера основан на использовании определителей и позволяет найти решение системы линейных уравнений с помощью отношения определителей матриц. Однако, для применения этого метода необходимо, чтобы матрица системы была квадратной и ее определитель не равнялся нулю.

2. Метод Гаусса

Метод Гаусса основан на приведении матрицы системы к ступенчатому виду и позволяет найти базисные переменные и свободные переменные системы. Затем, используя обратный ход Гаусса, можно получить все решения системы.

3. Метод Жордана–Гаусса

Метод Жордана–Гаусса является модификацией метода Гаусса и заключается в приведении матрицы системы к улучшенному ступенчатому виду. Этот метод также позволяет найти базисные переменные и свободные переменные системы и получить все ее решения.

4. Метод пристрелки

Метод пристрелки применяется в случае, когда система имеет бесконечное множество решений. Он основан на последовательном приближении к решению и нахождении значения свободной переменной, которая вводится к исходной системе.

5. Методы матричных вычислений

Методы матричных вычислений, такие как метод Гаусса-Жордана, метод Гаусса-Зейделя и методы LU-разложения, также могут использоваться для решения систем линейных уравнений.

Каждый из перечисленных методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной системы линейных уравнений, а также от поставленной задачи.

Примеры систем уравнений с бесконечным множеством решений

Примером системы уравнений с бесконечным множеством решений может быть:

Пример 1:

Система уравнений:

2x + 3y = 8

4x + 6y = 16

Эта система уравнений имеет бесконечное множество решений. Уравнения являются линейно зависимыми, так как удовлетворяют условию: одно уравнение можно получить, умножив другое на константу. В данном случае, первое уравнение можно получить, умножив второе на 0.5:

2x + 3y = 8

Таким образом, каждое значение x и y, удовлетворяющее первому уравнению, также удовлетворяет второму. Это дает бесконечное множество решений системы уравнений.

Пример 2:

Система уравнений:

3x + 2y = 7

6x + 4y = 14

Эта система уравнений также имеет бесконечное множество решений. Уравнения являются линейно зависимыми, так как удовлетворяют условию: одно уравнение можно получить, умножив другое на константу. В данном случае, первое уравнение можно получить, умножив второе на 0.5: