Касательная к графику – это линия, которая касается графика функции в определенной точке. Она является крайним случаем секущей прямой, когда эта прямая сходится к некоторой точке на графике. Параллельная оси абсцисс – это горизонтальная прямая, которая никогда не пересекает ось абсцисс и всегда расположена на одной и той же высоте. Как и в случае с обычными касательными, касательная к графику, параллельная оси абсцисс, также имеет важное значение в математике и физике.
Касательная к графику, параллельная оси абсцисс, играет важную роль при изучении поведения функций вокруг определенных точек. Она позволяет определить наклон графика в данной точке и предсказать его поведение в окрестности этой точки. Используя касательные, можно определить направление роста или убывания функции, а также точки максимума или минимума.
Одним из примеров, где касательная к графику, параллельная оси абсцисс, находит применение, является анализ движения тела по графику его положения от времени. Зная уравнение траектории движения, можно определить скорость и ускорение тела в определенный момент времени, используя касательные к графику скорости и ускорения. Таким образом, касательная к графику, параллельная оси абсцисс, помогает нам лучше понять различные аспекты функций и их поведение в разных точках.
Определение касательной к графику

Для того чтобы найти касательную к графику функции в определенной точке, мы можем использовать определенную формулу. Возьмем произвольную функцию f(x) и точку (a, f(a)), через которую нас интересует прямая касательная. Тогда касательная имеет уравнение:
| уравнение касательной: | y - f(a) = f'(a)(x - a) |
Где f'(a) представляет собой производную функции f(x) в точке a.
Полученное уравнение касательной позволяет нам определить наклон касательной в заданной точке и тем самым понять, является ли график функции в данной точке возрастающим или убывающим.
Определение касательной к графику функции позволяет нам лучше понять его свойства и поведение вблизи определенных точек. Кроме того, касательная также имеет множество практических применений в разных областях, таких как физика, экономика, и инженерия.
Касательная к графику и ее свойства
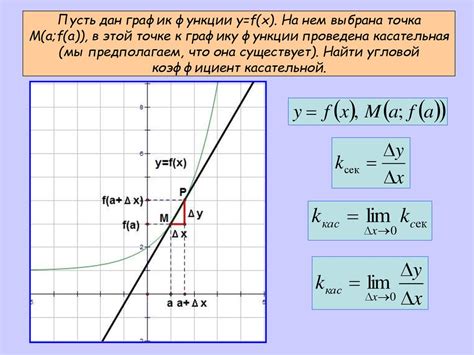
Свойства касательной к графику функции:
- Касательная к графику проходит через точку касания.
- Касательная к графику параллельна оси абсцисс при условии нулевого наклона функции в данной точке.
- Касательная к графику имеет наклон, равный производной функции в точке касания. Если производная положительна, касательная будет наклонена вправо, если отрицательна – влево.
- Касательная к графику является линейной функцией и может быть представлена уравнением прямой.
Касательные к графику играют важную роль в анализе функций и исследовании их поведения в различных точках. Они позволяют определить экстремумы функции, нули производной, границы области определения и другие характеристики.
Геометрическое представление касательной
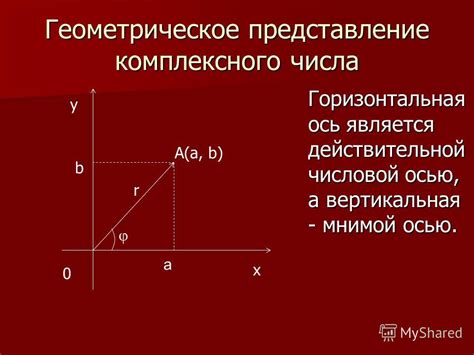
Касательная к графику функции представляет собой прямую линию, которая касается графика только в одной точке. Ее наклон определяется производной функции в этой точке.
Для построения касательной к графику функции в определенной точке необходимо знать координаты этой точки и значение производной функции в ней. Если производная положительна, то касательная наклонена вверх, если же производная отрицательна, то касательная наклонена вниз.
Если производная равна нулю, то касательная горизонтальна. В этом случае график функции имеет экстремум в данной точке.
Касательная к графику функции, параллельная оси абсцисс, имеет наклон, равный нулю. Такая касательная проходит через точку на оси абсцисс, находящуюся на том же уровне, что и точка касания.
Геометрическое представление касательной позволяет анализировать поведение функции вблизи каждой точки графика. Это важный инструмент при изучении функций и определении их свойств.
Нахождение уравнения касательной

Уравнение касательной к графику функции находится с использованием производной этой функции. Производная функции показывает наклон графика в каждой точке. Касательная к графику функции будет иметь тот же наклон, что и график в этой точке.
Для того чтобы найти уравнение касательной к графику функции, нужно выполнить следующие шаги:
- Найдите производную функции.
- Подставьте в полученное уравнение значение x, соответствующее точке, в которой нужно найти касательную.
- Найдите значение производной функции в этой точке.
- Подставьте полученное значение производной и значение x в уравнение прямой с наклоном, найденным в предыдущем пункте. Получите уравнение касательной.
Таким образом, уравнение касательной к графику функции y = f(x) в точке (x0, f(x0)) будет выглядеть как y = f'(x0)(x - x0) + f(x0). В этом уравнении f'(x0) - значение производной функции в точке x0.
Для наглядности можно построить таблицу, в которой будут представлены значения x, y, f'(x) и уравнение касательной в каждой точке.
| x | y | f'(x) | Уравнение касательной |
|---|---|---|---|
| x0 | y0 | f'(x0) | y = f'(x0)(x - x0) + y0 |
| x1 | y1 | f'(x1) | y = f'(x1)(x - x1) + y1 |
| x2 | y2 | f'(x2) | y = f'(x2)(x - x2) + y2 |
| ... | ... | ... | ... |
Таким образом, мы можем найти уравнение касательной для любой точки на графике функции. Это уравнение позволяет нам определить наклон и положение касательной относительно оси абсцисс.
Примеры задач на нахождение касательной

Ниже приведены несколько примеров задач, связанных с нахождением касательной к графику функции, параллельной оси абсцисс.
| Пример задачи | Решение |
|---|---|
Найти уравнение касательной линии к графику функции y = x^2 - 3 в точке (2, 1). | Для нахождения касательной линии к графику функции в заданной точке, следует воспользоваться производной функции. Производная функции y = x^2 - 3 равна y' = 2x. В точке (2, 1) значение производной равно 2*2 = 4. Значит, уравнение касательной линии имеет вид y - 1 = 4(x - 2). |
Найти уравнение касательной линии к графику функции y = 5x^3 + 2x^2 в точке (-1, -3). | Аналогично предыдущему примеру, вычисляем производную функции y = 5x^3 + 2x^2. Получаем y' = 15x^2 + 4x. Подставляем значение -1 для x в производную и находим значение равное 11. Получаем уравнение касательной линии y + 3 = 11(x + 1). |
Касательная к графику и производная функции
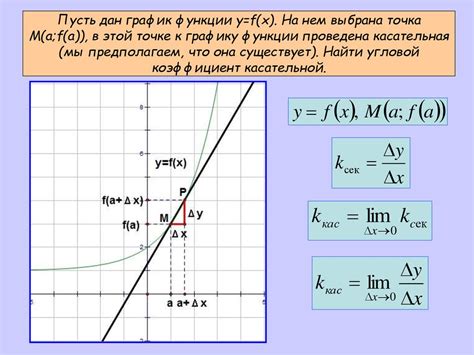
Определение касательной основано на производной функции. Производная функции описывает скорость изменения функции в каждой точке. Если значение производной функции в точке равно нулю, то это означает, что график функции имеет горизонтальную касательную в этой точке. Если значение производной функции в точке не равно нулю, то это означает, что график функции имеет наклонную (несколько отклоненную от горизонтальной) касательную в этой точке.
Для нахождения касательной к графику функции в определенной точке необходимо:
- Вычислить значение производной функции в этой точке.
- Подставить координаты точки и значение производной в формулу касательной прямой: y - y0 = m(x - x0), где m - значение производной, (x0, y0) - координаты точки на графике.
Таким образом, касательная к графику функции позволяет определить наклон функции в заданной точке. Использование производной функции позволяет вычислить наклон этой касательной и более точно оценить поведение функции в её окрестности.
Применение касательной в реальной жизни

Концепция касательной, параллельной оси абсцисс, имеет широкое применение в различных областях реальной жизни. Вот несколько примеров, где это применение играет важную роль:
1. Финансовый анализ
В финансовом анализе применяются графики для визуализации данных о доходах и расходах. Зная направление и угол наклона касательной в определенной точке графика доходов или расходов, можно предсказать тенденции и изменения в финансовых показателях.
2. Медицинское исследование
В медицинском исследовании, касательные к графикам используются для анализа изменений в показателях здоровья пациентов. Например, касательная к графику изменения веса позволяет оценить темпы его изменения, что может быть важным при диагностике некоторых заболеваний.
3. Инженерия и строительство
В инженерии и строительстве, касательные используются для оценки градиента и скорости изменения различных параметров. Например, в строительстве дороги, зная касательную к графику высоты относительно расстояния, можно определить уклон дороги и необходимость проведения дополнительных работ.
Это только некоторые примеры применения касательной в реальной жизни. В общем, умение анализировать и использовать касательные к графикам позволяет получить дополнительную информацию и делать прогнозы на основе имеющихся данных.
Преимущества использования касательной в графике
1. Определение точного значения функции:
Касательная предоставляет возможность находить точные значения функции в определенной точке графика. Это особенно полезно в случаях, когда для нас важно точное значение функции в определенной точке, например, при определении скорости, уклона или изменения функции в данной точке.
2. Анализ поведения функции:
Касательная позволяет провести анализ поведения функции вблизи определенной точки. С помощью касательной можно определить, является ли функция возрастающей или убывающей, имеет ли она точку экстремума или точку перегиба.
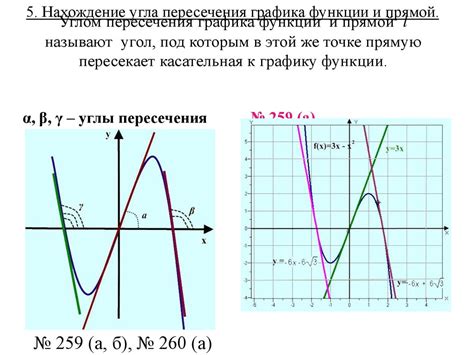
3. Решение геометрических задач:
Касательная может быть использована для решения различных геометрических задач. Например, с помощью касательной можно найти угол между касательной и другими линиями, определить точки пересечения графика с другими прямыми или кривыми.
Использование касательной в графике позволяет получить более подробную информацию о функции и ее поведении в различных точках. Это полезный инструмент для анализа и изучения функций в математике, физике и других науках.



