При изучении функций одно из важнейших понятий – их положительность. Знание об этом свойстве функций позволяет решать широкий круг задач, связанных с определением их поведения и нахождением экстремумов. Мы можем говорить о положительности функции в контексте всего множества аргументов или только в некоторой области. В любом случае, существуют определенные правила, позволяющие найти положительность функции и определить знак ее производной.
Один из способов определить положительность функции в точке - это анализ знаков. Изучая поведение функции вблизи точки, можно определить, как знак ее значения меняется справа налево или слева направо. Если функция возрастает, то говорят, что она положительна, и наоборот: если функция убывает, то она отрицательна. Это правило базируется на определении производной и использовании метода дифференцирования.
Также, существует частный случай, когда функция не изменяет знака на некотором интервале. В этом случае говорят, что функция строго положительна или строго отрицательна на этом интервале. Для определения знаков производной применяются правила дифференцирования, методы анализов с учетом особенностей функции и ее значений в крайних точках интервала.
Определение положительности функции

Для определения положительности функции в заданной точке необходимо проанализировать знак функции в данной точке и в окрестности этой точки.
Правила определения положительности функции:
- Если в некоторой окрестности точки, функция принимает положительные значения, то функция положительна в этой точке.
- Если в некоторой окрестности точки, функция принимает отрицательные значения, то функция отрицательна в этой точке.
- Если функция меняет знак при переходе через точку (функция имеет одинаковые значения с разных сторон точки), то функция имеет нулевое значение в этой точке.
Для более точного определения положительности функции, необходимо учитывать и другие свойства функции, такие как непрерывность, монотонность, наличие экстремумов.
Определение положительности функции в конкретных точках позволяет более точно анализировать поведение функции и применять это знание, например, при решении уравнений или оптимизационных задач.
Основной критерий положительности функции
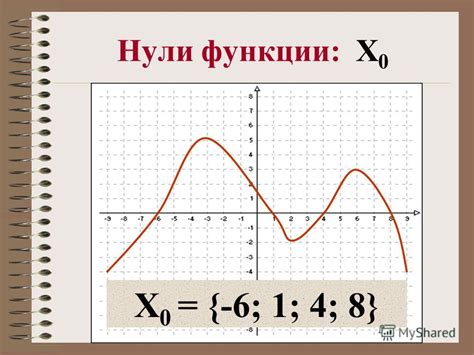
Основной критерий положительности функции заключается в нахождении интервалов, на которых функция принимает положительные значения.
Для этого необходимо решить неравенство:
f(x) > 0
Найденные интервалы будут являться областями положительности функции.
Основной критерий положительности функции применяется при исследовании функций на монотонность, а также для определения областей, где функция возрастает.
Имея информацию о положительности функции, мы можем строить график функции и использовать эту информацию для более глубокого анализа функции и ее свойств.
Знак производной и положительность функции

Если производная функции положительна на некотором интервале, то это означает, что функция возрастает на этом интервале. И наоборот, если производная функции отрицательна на некотором интервале, то функция убывает на этом интервале.
Знак производной также позволяет определить экстремумы функции. В точке, где производная равна нулю, функция может иметь экстремум – максимум или минимум.
Если производная меняет знак с плюса на минус, то это означает, что функция достигает максимума. А если производная меняет знак с минуса на плюс, то функция достигает минимума.
Однако стоит помнить, что знак производной не определяет положительность функции вне указанных интервалов. Для определения положительности функции вне этих интервалов необходимо провести дополнительные исследования, такие как анализ поведения функции на бесконечностях или на конечных точках.
Итак, знак производной является важным инструментом для определения положительности функции и нахождения её экстремумов, однако для полного анализа функции может потребоваться проведение дополнительных исследований.
Условия существования производной для положительной функции

Для того чтобы функция имела производную в точке и сохраняла свою положительность, необходимо, чтобы выполнялись следующие условия:
- Функция должна быть непрерывной в данной точке и на некоторой окрестности этой точки.
- Функция должна быть определена и положительна в данной точке и на некоторой окрестности этой точки.
- Предел функции при приближении к данной точке должен существовать и быть конечным.
Если все эти условия выполняются, то говорят, что функция имеет производную в данной точке и сохраняет свою положительность.
Определение положительности производной

Для определения положительности производной функции в определенной точке необходимо провести следующие шаги:
- Найти производную функции.
- Подставить значение точки в полученную производную.
- Если полученное значение положительное, то производная положительна в данной точке. Если значение отрицательное, то производная отрицательна. Если же значение равно нулю, то необходимо проводить дополнительные исследования с помощью других методов.
Данный алгоритм позволяет определить положительность производной для функции в заданной точке, что может быть полезным в различных математических и физических задачах.
Положительная производная и возрастание функции
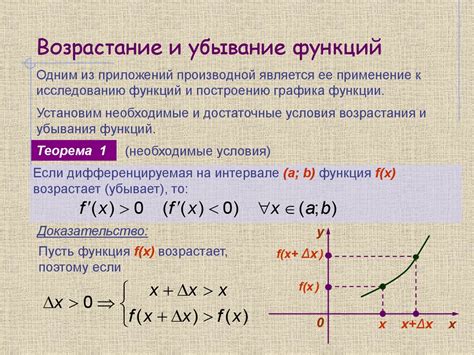
Если производная функции положительна на некотором интервале, то можно сказать, что функция возрастает на этом интервале. Это означает, что значения функции на данном интервале увеличиваются при увеличении аргумента.
Для определения, является ли производная положительной на интервале, необходимо выполнить следующие шаги:
- Найти производную функции.
- Решить неравенство полученной производной, приравняв ее к нулю и определив интервалы, на которых производная положительна либо отрицательна.
Например, пусть дана функция f(x) = 2x^3 - 3x^2 + 1. Найдем производную функции: f'(x) = 6x^2 - 6x. Решим уравнение f'(x) = 0:
| 6x^2 - 6x | = | 0 |
|---|---|---|
| 6x(x - 1) | = | 0 |
Получаем два корня: x = 0 и x = 1. Определим знак производной на интервалах (-∞, 0), (0, 1) и (1, +∞). Для этого выберем произвольные значения x из каждого интервала и подставим их в производную:
- Выбираем x = -1. Подставляем в производную: f'(-1) = 6(-1)^2 - 6(-1) = 12. Знак положительный, значит на интервале (-∞, 0) производная положительная и функция возрастает.
- Выбираем x = 0. Подставляем в производную: f'(0) = 6(0)^2 - 6(0) = 0. Знак равен нулю, значит на интервале (0, 1) производная равна нулю и функция имеет экстремум.
- Выбираем x = 2. Подставляем в производную: f'(2) = 6(2)^2 - 6(2) = 12. Знак положительный, значит на интервале (1, +∞) производная положительная и функция возрастает.
Итак, функция f(x) = 2x^3 - 3x^2 + 1 возрастает на интервалах (-∞, 0) и (1, +∞), а на интервале (0, 1) имеет экстремум.
График функции и положительности производной
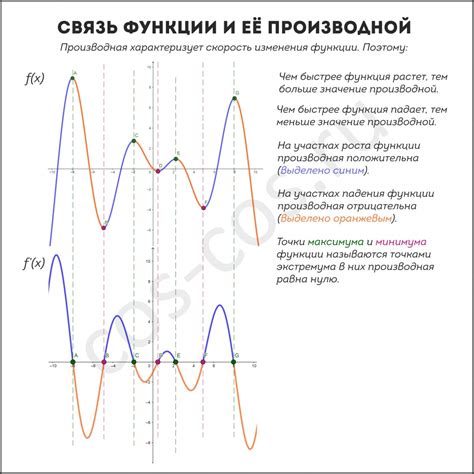
Для определения положительности функции на заданном интервале, необходимо проанализировать график функции на этом интервале. Если график функции на этом интервале находится выше оси абсцисс (горизонтальной оси), то функция положительна на данном интервале. Если график функции находится ниже оси абсцисс, то функция отрицательна на данном интервале.
График производной функции также имеет большое значение при определении положительности функции. Если график производной функции на заданном интервале находится выше оси абсцисс, то функция возрастает на данном интервале и, следовательно, положительна. Если график производной функции находится ниже оси абсцисс, то функция убывает на данном интервале и, следовательно, отрицательна.
| Функция | График функции | Производная | График производной | Положительность функции |
|---|---|---|---|---|
| Функция 1 | График функции 1 | Производная 1 | График производной 1 | Функция 1 положительна на интервале [a, b] |
| Функция 2 | График функции 2 | Производная 2 | График производной 2 | Функция 2 отрицательна на интервале [c, d] |
Связь между положительностью функции и производной

Функция положительна, если ее значения всегда больше нуля на определенном интервале или на всей области определения. Положительность функции означает, что она лежит выше оси OX и не пересекает ее.
Производная функции показывает ее скорость изменения в каждой точке. Если производная положительна на определенном интервале или на всей области определения, то функция возрастает. Это означает, что с увеличением значения аргумента функция также увеличивается. Если производная отрицательна, то функция убывает, уменьшаясь с ростом значения аргумента.
Связь между положительностью функции и производной заключается в том, что если производная функции положительна на определенном интервале, то сама функция положительна на этом интервале. Аналогично, если производная отрицательна на интервале, то функция отрицательна на этом интервале. Однако, если производная равна нулю на интервале, это не означает, что функция всегда положительна или отрицательна на этом интервале.
Пример: Рассмотрим функцию f(x) = x^2. Ее производная равна f'(x) = 2x. Очевидно, что производная положительна для всех положительных значений x, а значит, функция возрастает на всей области определения (положительна на интервале (0, +∞)).
Практическое применение положительности функции и производной

Определение положительности функции и ее производной имеет широкое применение в различных областях математики и ее приложениях. Этот аналитический инструмент позволяет получить полезную информацию о поведении функции и ее изменении на определенном интервале.
Одним из основных применений является определение экстремумов функции. Анализ положительности производной позволяет найти точки, в которых функция достигает своих локальных минимумов и максимумов. Если производная положительна на интервале, то функция возрастает, а если производная отрицательна, то функция убывает. Точки, в которых производная равна нулю, называются критическими точками, где может находиться экстремум функции.
Еще одним применением положительности функции является определение ее выпуклости и вогнутости. Если производная функции положительна на интервале, то функция является выпуклой на этом интервале. Если производная отрицательна, то функция является вогнутой. Эта информация позволяет оценить форму и поведение графика функции, а также прогнозировать возможные точки перегиба и экстремумы.
В общем случае, положительность функции и ее производной предоставляют информацию о изменении функциональных величин, что позволяет анализировать и прогнозировать различные явления и процессы в науке, инженерии и экономике. Благодаря этому аналитическому инструменту можно оптимизировать системы, повысить эффективность и эффективно управлять различными процессами.
Важно отметить, что умение корректно интерпретировать и использовать положительность функции и ее производной в конкретных ситуациях является критически важным навыком для успешного решения математических задач и практических проблем.
Примеры задач с положительностью функции и производной

Пример 1:
Дана функция f(x) = x^2 - 2x + 1. Найдите интервалы, на которых функция положительна.
Решение:
Найдем производную функции: f'(x) = 2x - 2. Чтобы найти интервалы положительности функции, нам нужно решить неравенство f'(x) > 0.
2x - 2 > 0
2x > 2
x > 1
Таким образом, функция f(x) положительна на интервале (1, +∞).
Пример 2:
Дана функция g(x) = x^3 - 6x^2 + 11x - 6. Найдите значения x, при которых функция положительна.
Решение:
Найдем производную функции: g'(x) = 3x^2 - 12x + 11. Чтобы найти значения x, при которых функция положительна, нам нужно решить неравенство g'(x) > 0.
3x^2 - 12x + 11 > 0
Данное квадратное неравенство можно решить, используя метод интервалов или графический метод. В результате анализа, мы получаем, что функция g(x) положительна на интервалах (-∞, 1) и (3, +∞).
Пример 3:
Дана функция h(x) = sin(x) - cos(x). Найдите интервалы, на которых функция положительна.
Решение:
Найдем производную функции: h'(x) = cos(x) + sin(x). Для нахождения интервалов положительности функции, решим неравенство h'(x) > 0.
cos(x) + sin(x) > 0
С помощью графического метода мы можем увидеть, что функция h(x) положительна на интервалах (0, π/4) и (5π/4, 2π).
Таким образом, положительность функции и ее производной играют важную роль при анализе графиков и поведения функций. Они помогают определить интервалы, на которых функции положительны и найти точки, где функция меняет свой знак. Это особенно полезно при решении задач на определение экстремумов функций, нахождение корней и построение графиков.



